Finance Analysis

Timetk is designed to work with any time series domain. Arguably the most important is Finance. This tutorial showcases how you can perform Financial Investment and Stock Analysis at scale with pytimetk. This applied tutorial covers financial analysis with:

tk.plot_timeseries(): Visualizing financial data
tk.augment_rolling(): Moving averages
tk.augment_rolling_apply(): Rolling correlations and rolling regressions

Load the following packages before proceeding with this tutorial.

Code

import pytimetk as tk
import pandas as pd
import numpy as np

1 3 Core Properties: Financial Data

Financial data from sources like openbb or yfinance come in OHLCV format and typically include an “adjusted” price (adjusted for stock splits). This data has the 3 core properties of time series:

Timestamp: daily, hourly frequencies
Value: A price (or returns)
Groups: Stock symbols

Let’s take a look with the tk.glimpse() function.

Code

stocks_df = tk.load_dataset("stocks_daily", parse_dates = ['date'])

stocks_df.glimpse()

<class 'pandas.core.frame.DataFrame'>: 16194 rows of 8 columns
symbol:    object            ['META', 'META', 'META', 'META', 'META', 'M ...
date:      datetime64[ns]    [Timestamp('2013-01-02 00:00:00'), Timestam ...
open:      float64           [27.440000534057617, 27.8799991607666, 28.0 ...
high:      float64           [28.18000030517578, 28.46999931335449, 28.9 ...
low:       float64           [27.420000076293945, 27.59000015258789, 27. ...
close:     float64           [28.0, 27.770000457763672, 28.7600002288818 ...
volume:    int64             [69846400, 63140600, 72715400, 83781800, 45 ...
adjusted:  float64           [28.0, 27.770000457763672, 28.7600002288818 ...

2 Visualizing Financial Data

Visualizing financial data is critical for:

Quick Insights
Enhanced Decision Making
Performance Monitoring
Ease of Reporting

We can visualize financial data over time with tk.plot_timeseries():

An interactive plotly plot is returned by default. A static plot can be returned by setting engine = "plotnine".
A blue smoother is added by default. The smoother can be removed with smooth = False.

Getting More Info: tk.plot_timeseries()

Click here to see our Data Visualization Guide
Use help(tk.plot_timeseries) to review additional helpful documentation.

Plotly
Plotnine

An interactive plotly plot is returned by default. Interactive is useful for fast data exploration and for use in web apps (e.g. streamlit, shiny, dash), Click to expand code template.

Code

# plotly engine
stocks_df \
    .groupby('symbol') \
    .plot_timeseries(
        'date', 'adjusted',
        facet_ncol = 2,
        smooth = True,
        smooth_frac = 0.10,
        width = 900,
        height = 700,
        engine = 'plotly',
    )

You can quickly change to a static plot using the plotnine or matplotlib engines. This returns a professional facetted stock chart useful for financial reports. Click to expand code template.

Code

# plotnine engine
stocks_df \
    .groupby('symbol') \
    .plot_timeseries(
        'date', 'adjusted',
        facet_ncol = 2,
        smooth = True,
        smooth_frac = 0.10,
        width = 900,
        height = 700,
        engine = 'plotnine'
    )

<Figure Size: (900 x 700)>

3 Technical Indicators

Technical indicators are mathematical calculations based on the price, volume, or open interest of a security or contract used by traders who follow technical analysis. Technical analysis is a method of forecasting the direction of financial market prices through the study of past market data, primarily price, and volume. Technical indicators are most extensively used in the context of the stock market but are also used in other financial markets like forex, commodities, and cryptocurrencies.

Types of Technical Indicators:

Trend Indicators:
- Moving Averages: Helps smooth out price data to form a single flowing line, identifying the direction of the trend.
- Moving Average Convergence Divergence (MACD): Shows the relationship between two moving averages of a security’s price.
- Average True Range (ATR): Measures market volatility.
Momentum Indicators:
- Relative Strength Index (RSI): Measures the speed and change of price movements, typically on a scale of 1 to 100.
- Stochastic Oscillator: Compares a security’s closing price to its price range over a specific period.
Volume Indicators:
- On-Balance Volume (OBV): Uses volume flow to predict changes in stock price.
- Accumulation/Distribution Line: Looks at the proximity of closing prices to their highs or lows to determine if accumulation or distribution is occurring in the market.
Volatility Indicators:
- Bollinger Bands: Consist of a middle band being an N-period simple moving average (SMA), an upper band at K times an N-period standard deviation above the middle band, and a lower band at K times an N-period standard deviation below the middle band.
- Average True Range (ATR): Provides a measure of a market’s volatility.
Market Strength Indicators:
- Advance/Decline Line: Represents the number of advancing stocks divided by the number of declining stocks over a given period.
- Market Breadth: Measures the number of securities that have advanced and declined in a specific market or index, giving traders a feel for the market’s overall mood.

Let’s see a few examples of technical indicators in pytimetk.

3.1 Application: Moving Averages, 10-Day and 50-Day

This code template can be used to make and visualize the 10-day and 50-Day moving average of a group of stock symbols. Click to expand the code.

Plotly
Plotnine

Code

# Add 2 moving averages (10-day and 50-Day)
sma_df = stocks_df[['symbol', 'date', 'adjusted']] \
    .groupby('symbol') \
    .augment_rolling(
        date_column = 'date',
        value_column = 'adjusted',
        window = [10, 50],
        window_func = ['mean'],
        center = False,
        threads = 1, # Change to -1 to use all available cores
    )

# Visualize 
(sma_df 

    # zoom in on dates
    .query('date >= "2023-01-01"') 

    # Convert to long format
    .melt(
        id_vars = ['symbol', 'date'],
        value_vars = ["adjusted", "adjusted_rolling_mean_win_10", "adjusted_rolling_mean_win_50"]
    ) 

    # Group on symbol and visualize
    .groupby("symbol") 
    .plot_timeseries(
        date_column = 'date',
        value_column = 'value',
        color_column = 'variable',
        smooth = False, 
        facet_ncol = 2,
        width = 900,
        height = 700,
        engine = "plotly"
    )
)

Code

# Add 2 moving averages (10-day and 50-Day)
sma_df = stocks_df[['symbol', 'date', 'adjusted']] \
    .groupby('symbol') \
    .augment_rolling(
        date_column = 'date',
        value_column = 'adjusted',
        window = [10, 50],
        window_func = ['mean'],
        center = False,
        threads = 1, # Change to -1 to use all available cores
    )

# Visualize 
(sma_df 

    # zoom in on dates
    .query('date >= "2023-01-01"') 

    # Convert to long format
    .melt(
        id_vars = ['symbol', 'date'],
        value_vars = ["adjusted", "adjusted_rolling_mean_win_10", "adjusted_rolling_mean_win_50"]
    ) 

    # Group on symbol and visualize
    .groupby("symbol") 
    .plot_timeseries(
        date_column = 'date',
        value_column = 'value',
        color_column = 'variable',
        smooth = False, 
        facet_ncol = 2,
        width = 900,
        height = 700,
        engine = "plotnine"
    )
)

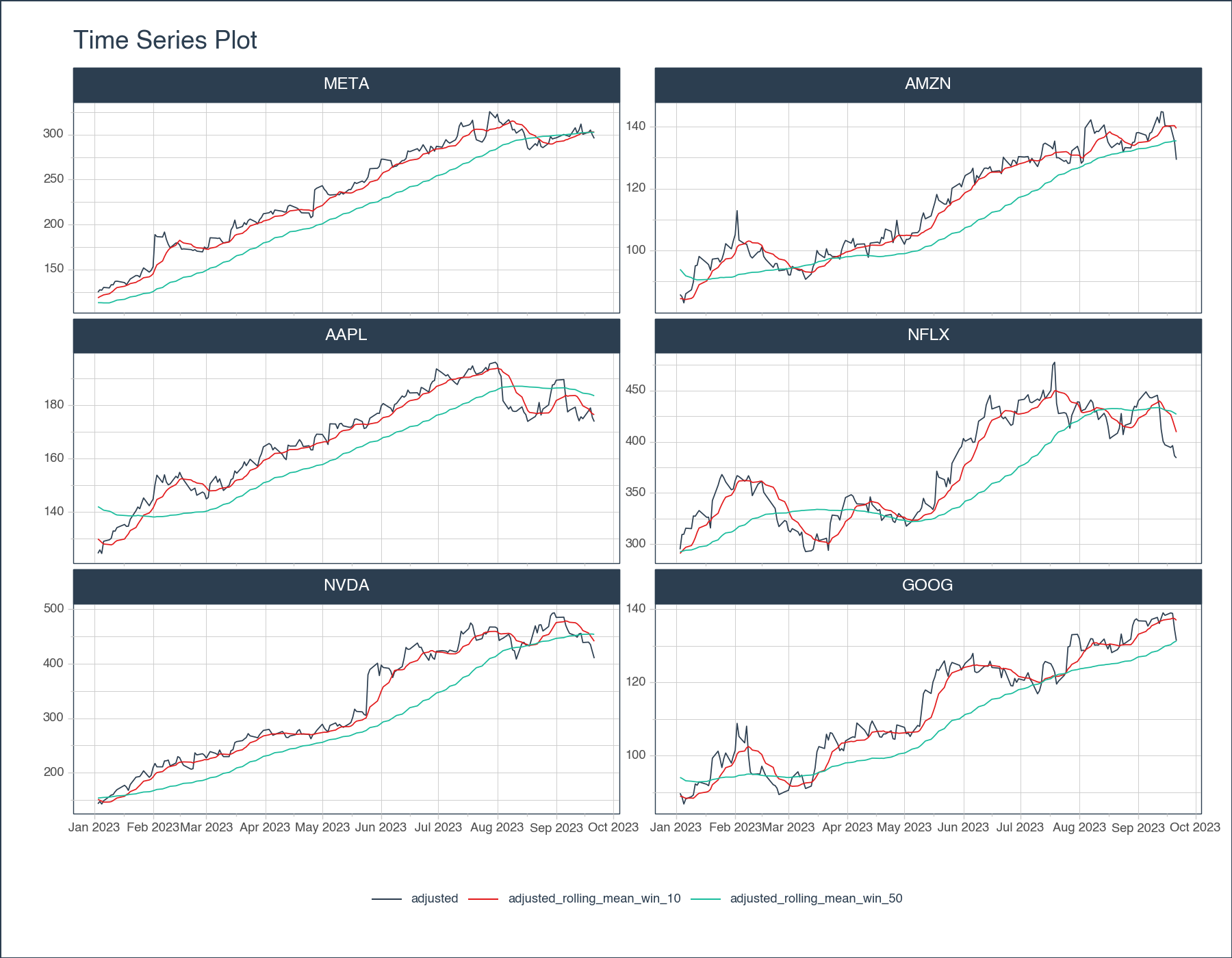
<Figure Size: (900 x 700)>

3.2 Application: Bollinger Bands

Bollinger Bands are a volatility indicator commonly used in financial trading. They consist of three lines:

The middle band, which is a simple moving average (usually over 20 periods).
The upper band, calculated as the middle band plus k times the standard deviation of the price (typically, k=2).
The lower band, calculated as the middle band minus k times the standard deviation of the price.

Here’s how you can calculate and plot Bollinger Bands with pytimetk using this code template (click to expand):

Plotly
Plotnine

Code

# Bollinger Bands
bollinger_df = stocks_df[['symbol', 'date', 'adjusted']] \
    .groupby('symbol') \
    .augment_rolling(
        date_column = 'date',
        value_column = 'adjusted',
        window = 20,
        window_func = ['mean', 'std'],
        center = False
    ) \
    .assign(
        upper_band = lambda x: x['adjusted_rolling_mean_win_20'] + 2*x['adjusted_rolling_std_win_20'],
        lower_band = lambda x: x['adjusted_rolling_mean_win_20'] - 2*x['adjusted_rolling_std_win_20']
    )


# Visualize
(bollinger_df

    # zoom in on dates
    .query('date >= "2023-01-01"') 

    # Convert to long format
    .melt(
        id_vars = ['symbol', 'date'],
        value_vars = ["adjusted", "adjusted_rolling_mean_win_20", "upper_band", "lower_band"]
    ) 

    # Group on symbol and visualize
    .groupby("symbol") 
    .plot_timeseries(
        date_column = 'date',
        value_column = 'value',
        color_column = 'variable',
        # Adjust colors for Bollinger Bands
        color_palette =["#2C3E50", "#E31A1C", '#18BC9C', '#18BC9C'],
        smooth = False, 
        facet_ncol = 2,
        width = 900,
        height = 700,
        engine = "plotly" 
    )
)

Code

# Bollinger Bands
bollinger_df = stocks_df[['symbol', 'date', 'adjusted']] \
    .groupby('symbol') \
    .augment_rolling(
        date_column = 'date',
        value_column = 'adjusted',
        window = 20,
        window_func = ['mean', 'std'],
        center = False
    ) \
    .assign(
        upper_band = lambda x: x['adjusted_rolling_mean_win_20'] + 2*x['adjusted_rolling_std_win_20'],
        lower_band = lambda x: x['adjusted_rolling_mean_win_20'] - 2*x['adjusted_rolling_std_win_20']
    )


# Visualize
(bollinger_df

    # zoom in on dates
    .query('date >= "2023-01-01"') 

    # Convert to long format
    .melt(
        id_vars = ['symbol', 'date'],
        value_vars = ["adjusted", "adjusted_rolling_mean_win_20", "upper_band", "lower_band"]
    ) 

    # Group on symbol and visualize
    .groupby("symbol") 
    .plot_timeseries(
        date_column = 'date',
        value_column = 'value',
        color_column = 'variable',
        # Adjust colors for Bollinger Bands
        color_palette =["#2C3E50", "#E31A1C", '#18BC9C', '#18BC9C'],
        smooth = False, 
        facet_ncol = 2,
        width = 900,
        height = 700,
        engine = "plotnine"
    )
)

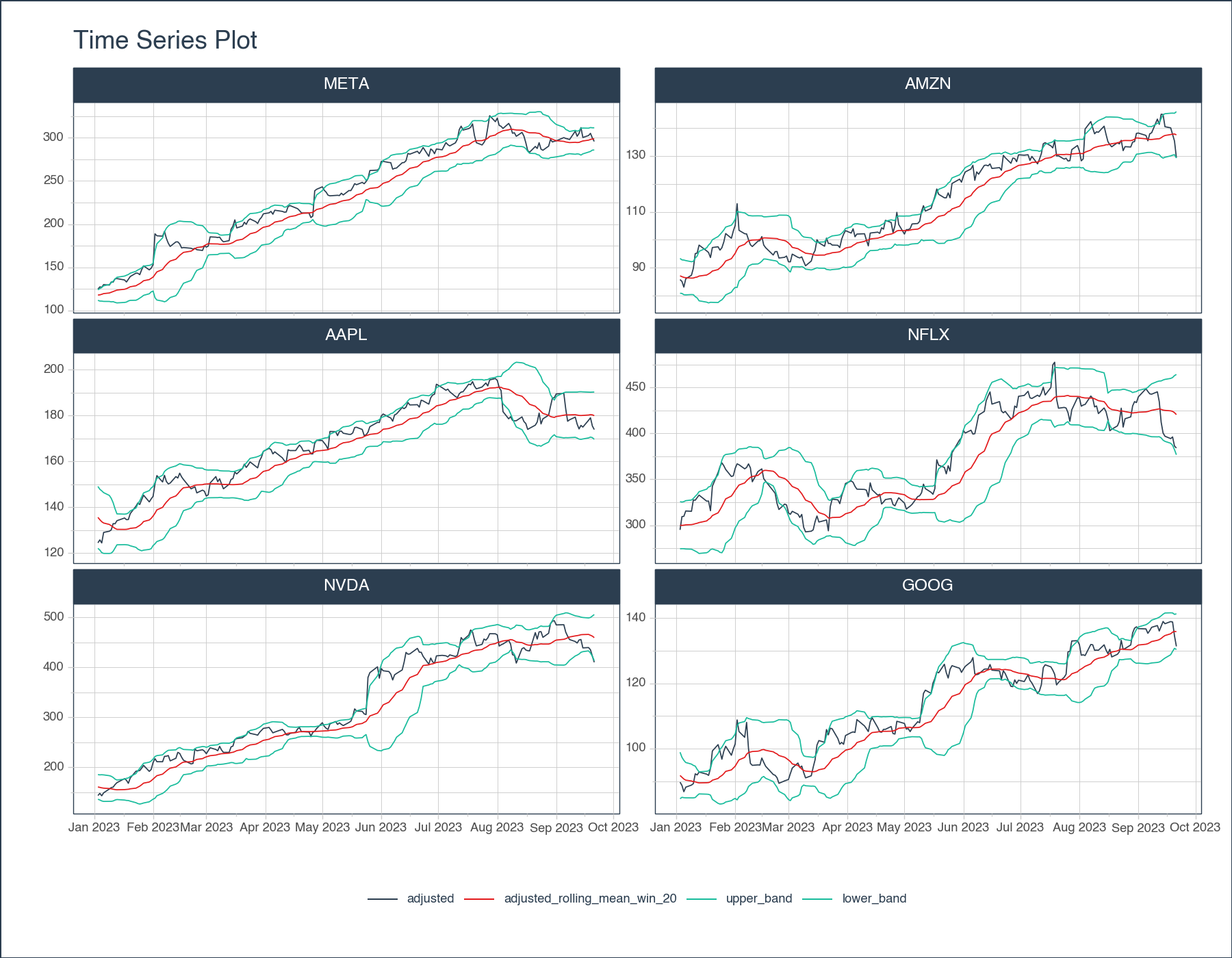
<Figure Size: (900 x 700)>

4 Returns Analysis

In finance, returns analysis involves evaluating the gains or losses made on an investment relative to the amount of money invested. It’s a critical aspect of investment and portfolio management:

Performance: Returns analysis determines the performance and the risk-reward profile of financial assets, portfolios, or investment strategies.
Informed Decision Making: Returns analysis allows investors, analysts, and portfolio managers to make informed decisions regarding asset allocation, risk management, and investment strategy.

4.1 Returns Analysis By Time

Returns are NOT static (so analyze them by time)

We can use rolling window calculations with tk.augment_rolling() to compute many rolling features at scale such as rolling mean, std, range (spread).
We can expand our tk.augment_rolling_apply() rolling calculations to Rolling Correlation and Rolling Regression (to make comparisons over time)

Application: Descriptive Statistic Analysis

Many traders compute descriptive statistics like mean, median, mode, skewness, kurtosis, and standard deviation to understand the central tendency, spread, and shape of the return distribution.

Step 1: Returns

Use this code to get the pct_change() in wide format. Click expand to get the code.

Code

returns_wide_df = stocks_df[['symbol', 'date', 'adjusted']] \
    .pivot(index = 'date', columns = 'symbol', values = 'adjusted') \
    .pct_change() \
    .reset_index() \
    [1:]

returns_wide_df

symbol	date	AAPL	AMZN	GOOG	META	NFLX	NVDA
1	2013-01-03	-0.012622	0.004547	0.000581	-0.008214	0.049777	0.000786
2	2013-01-04	-0.027854	0.002592	0.019760	0.035650	-0.006315	0.032993
3	2013-01-07	-0.005883	0.035925	-0.004363	0.022949	0.033549	-0.028897
4	2013-01-08	0.002691	-0.007748	-0.001974	-0.012237	-0.020565	-0.021926
5	2013-01-09	-0.015629	-0.000113	0.006573	0.052650	-0.012865	-0.022418
...	...	...	...	...	...	...	...
2694	2023-09-15	-0.004154	-0.029920	-0.004964	-0.036603	-0.008864	-0.036879
2695	2023-09-18	0.016913	-0.002920	0.004772	0.007459	-0.006399	0.001503
2696	2023-09-19	0.006181	-0.016788	-0.000936	0.008329	0.004564	-0.010144
2697	2023-09-20	-0.019992	-0.017002	-0.030541	-0.017701	-0.024987	-0.029435
2698	2023-09-21	-0.008889	-0.044053	-0.023999	-0.013148	-0.005566	-0.028931

2698 rows × 7 columns

Step 2: Descriptive Stats

Use this code to get standard statistics with the describe() method. Click expand to get the code.

Code

returns_wide_df.describe()

symbol	AAPL	AMZN	GOOG	META	NFLX	NVDA
count	2698.000000	2698.000000	2698.000000	2698.000000	2698.000000	2698.000000
mean	0.001030	0.001068	0.000885	0.001170	0.001689	0.002229
std	0.018036	0.020621	0.017267	0.024291	0.029683	0.028320
min	-0.128647	-0.140494	-0.111008	-0.263901	-0.351166	-0.187559
25%	-0.007410	-0.008635	-0.006900	-0.009610	-0.012071	-0.010938
50%	0.000892	0.001050	0.000700	0.001051	0.000544	0.001918
75%	0.010324	0.011363	0.009053	0.012580	0.014678	0.015202
max	0.119808	0.141311	0.160524	0.296115	0.422235	0.298067

Step 3: Correlation

And run a correlation with corr(). Click expand to get the code.

Code

corr_table_df = returns_wide_df.drop('date', axis=1).corr()
corr_table_df

symbol	AAPL	AMZN	GOOG	META	NFLX	NVDA
symbol
AAPL	1.000000	0.497906	0.566452	0.479787	0.321694	0.526508
AMZN	0.497906	1.000000	0.628103	0.544481	0.475078	0.490234
GOOG	0.566452	0.628103	1.000000	0.595728	0.428470	0.531382
META	0.479787	0.544481	0.595728	1.000000	0.407417	0.450586
NFLX	0.321694	0.475078	0.428470	0.407417	1.000000	0.380153
NVDA	0.526508	0.490234	0.531382	0.450586	0.380153	1.000000

The problem is that the stock market is constantly changing. And these descriptive statistics aren’t representative of the most recent fluctuations. This is where pytimetk comes into play with rolling descriptive statistics.

Application: 90-Day Rolling Descriptive Statistics Analysis with `tk.augment_rolling()`

Let’s compute and visualize the 90-day rolling statistics.

Getting More Info: tk.augment_rolling()

Click here to see our Augmenting Guide
Use help(tk.augment_rolling) to review additional helpful documentation.

Step 1: Long Format Pt.1

Use this code to get the date melt() into long format. Click expand to get the code.

Code

returns_long_df = returns_wide_df \
    .melt(id_vars='date', value_name='returns') 

returns_long_df

	date	symbol	returns
0	2013-01-03	AAPL	-0.012622
1	2013-01-04	AAPL	-0.027854
2	2013-01-07	AAPL	-0.005883
3	2013-01-08	AAPL	0.002691
4	2013-01-09	AAPL	-0.015629
...	...	...	...
16183	2023-09-15	NVDA	-0.036879
16184	2023-09-18	NVDA	0.001503
16185	2023-09-19	NVDA	-0.010144
16186	2023-09-20	NVDA	-0.029435
16187	2023-09-21	NVDA	-0.028931

16188 rows × 3 columns

Step 2: Augment Rolling Statistic

Let’s add multiple columns of rolling statistics. Click to expand the code.

Code

rolling_stats_df = returns_long_df \
    .groupby('symbol') \
    .augment_rolling(
        date_column = 'date',
        value_column = 'returns',
        window = [90],
        window_func = [
            'mean', 
            'std', 
            'min',
            ('q25', lambda x: np.quantile(x, 0.25)),
            'median',
            ('q75', lambda x: np.quantile(x, 0.75)),
            'max'
        ],
        threads = 1 # Change to -1 to use all threads
    ) \
    .dropna()

rolling_stats_df

	date	symbol	returns	returns_rolling_mean_win_90	returns_rolling_std_win_90	returns_rolling_min_win_90	returns_rolling_q25_win_90	returns_rolling_median_win_90	returns_rolling_q75_win_90	returns_rolling_max_win_90
89	2013-05-13	AAPL	0.003908	-0.001702	0.022233	-0.123558	-0.010533	-0.001776	0.012187	0.041509
90	2013-05-14	AAPL	-0.023926	-0.001827	0.022327	-0.123558	-0.010533	-0.001776	0.012187	0.041509
91	2013-05-15	AAPL	-0.033817	-0.001894	0.022414	-0.123558	-0.010533	-0.001776	0.012187	0.041509
92	2013-05-16	AAPL	0.013361	-0.001680	0.022467	-0.123558	-0.010533	-0.001360	0.013120	0.041509
93	2013-05-17	AAPL	-0.003037	-0.001743	0.022462	-0.123558	-0.010533	-0.001776	0.013120	0.041509
...	...	...	...	...	...	...	...	...	...	...
16183	2023-09-15	NVDA	-0.036879	0.005159	0.036070	-0.056767	-0.012587	-0.000457	0.018480	0.243696
16184	2023-09-18	NVDA	0.001503	0.005396	0.035974	-0.056767	-0.011117	0.000177	0.018480	0.243696
16185	2023-09-19	NVDA	-0.010144	0.005162	0.036006	-0.056767	-0.011117	-0.000457	0.018480	0.243696
16186	2023-09-20	NVDA	-0.029435	0.004953	0.036153	-0.056767	-0.012587	-0.000457	0.018480	0.243696
16187	2023-09-21	NVDA	-0.028931	0.004724	0.036303	-0.056767	-0.013166	-0.000457	0.018480	0.243696

15654 rows × 10 columns

Step 3: Long Format Pt.2

Finally, we can .melt() each of the rolling statistics for a Long Format Analysis. Click to expand the code.

Code

rolling_stats_long_df = rolling_stats_df \
    .melt(
        id_vars = ["symbol", "date"],
        var_name = "statistic_type"
    )

rolling_stats_long_df

	symbol	date	statistic_type	value
0	AAPL	2013-05-13	returns	0.003908
1	AAPL	2013-05-14	returns	-0.023926
2	AAPL	2013-05-15	returns	-0.033817
3	AAPL	2013-05-16	returns	0.013361
4	AAPL	2013-05-17	returns	-0.003037
...	...	...	...	...
125227	NVDA	2023-09-15	returns_rolling_max_win_90	0.243696
125228	NVDA	2023-09-18	returns_rolling_max_win_90	0.243696
125229	NVDA	2023-09-19	returns_rolling_max_win_90	0.243696
125230	NVDA	2023-09-20	returns_rolling_max_win_90	0.243696
125231	NVDA	2023-09-21	returns_rolling_max_win_90	0.243696

125232 rows × 4 columns

With the data formatted properly we can evaluate the 90-Day Rolling Statistics using .plot_timeseries().

Plotly
Plotnine

Code

rolling_stats_long_df \
    .groupby(['symbol', 'statistic_type']) \
    .plot_timeseries(
        date_column = 'date',
        value_column = 'value',
        facet_ncol = 6,
        width = 1500,
        height = 1000,
        title = "90-Day Rolling Statistics"
    )

1 3 Core Properties: Financial Data

2 Visualizing Financial Data

3 Technical Indicators

Types of Technical Indicators:

3.1 Application: Moving Averages, 10-Day and 50-Day

3.2 Application: Bollinger Bands

4 Returns Analysis

4.1 Returns Analysis By Time

Application: Descriptive Statistic Analysis

Step 1: Returns

Step 2: Descriptive Stats

Step 3: Correlation

Application: 90-Day Rolling Descriptive Statistics Analysis with tk.augment_rolling()

Step 1: Long Format Pt.1

Step 2: Augment Rolling Statistic

Step 3: Long Format Pt.2

Application: 90-Day Rolling Descriptive Statistics Analysis with `tk.augment_rolling()`